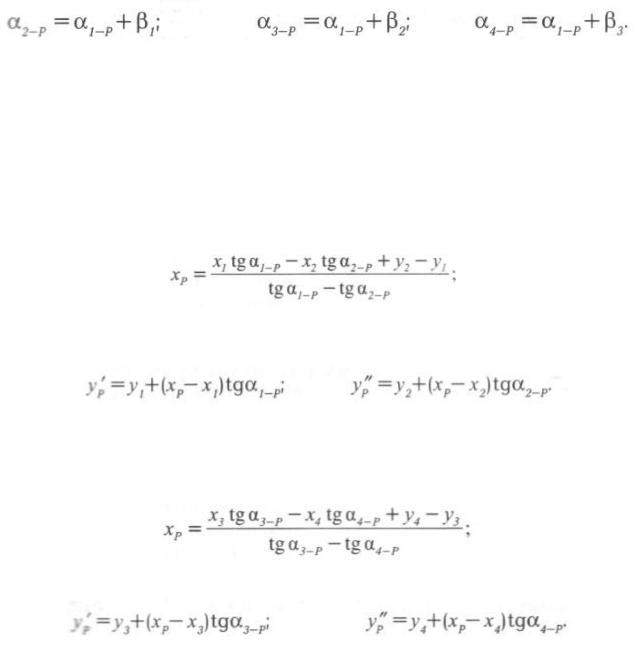Литература / Обратная геодезическая засечка
Задание 2. Обратная геодезическая засечка (задача Потенота)
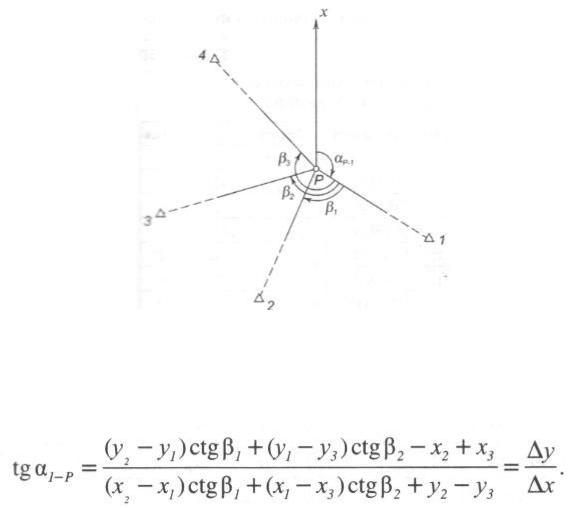
Сущность обратной геодезической засечки состоит в определении координат дополнительной точки P путем измерения на этой точке углов между направлениями как минимум на три исходных пункта с известными координатами. На практике для получения надежного контроля и повышения точности определения координат искомой точки используют многократную обратную засечку не менее чем по четырем исходным пунктам (рис. 1). В этом случаи решение обратной засечки выполняют независимо по двум комбинациям исходных пунктов (напр., пункты 1,2,3 и 1,3,4 ).
Следует помнить, что при решение обратной засечки исходные пункты нумеруют по часовой стрелке, считая наблюдателя (точка P) центром.
Из многочисленных способов и приемов решения задачи Потенота заданием предусмотрено решение обратной геодезической засечки по четырем исходным пунктам (см. рис. 1) способом Деламбра. Идея этого способа состоит в приведение решения обратной засечки к решению прямых засечек по формулам Гаусса. Для этого необходимо по имеющемся исходным данным найти дирекционные углы направлений с исходных пунктов на определяемую точку. Варианты решения задания приведены в приложении II.
Решение задачи способом Деламбра выполняют в следующей последовательности. 1. Вычисляют дирекционный угол направления с исходного пункта 1 на определяемую
точку P по формуле:
2. Определяют дирекционные углы направлений с других исходных пунктов ( 2,3,4 ):
3. Используя формулы тангенсов или котангенсов дирекционных углов направлений с исходных пунктов на определенную точку P (формулы Гаусса), вычисляют координаты точки P в двух комбинациях. Первое решение получают при использование дирекционных углов α 1-p и α 2-p ; для второго решения используют дирекционные углы α 3-p и α 4-p . Второе решение является контрольным и независимым от первого, так как угол β 3 , участвующий в определении дирекционного угла α 4-p , не использовался при вычеслении угла α 1-p по формуле Деламбра.
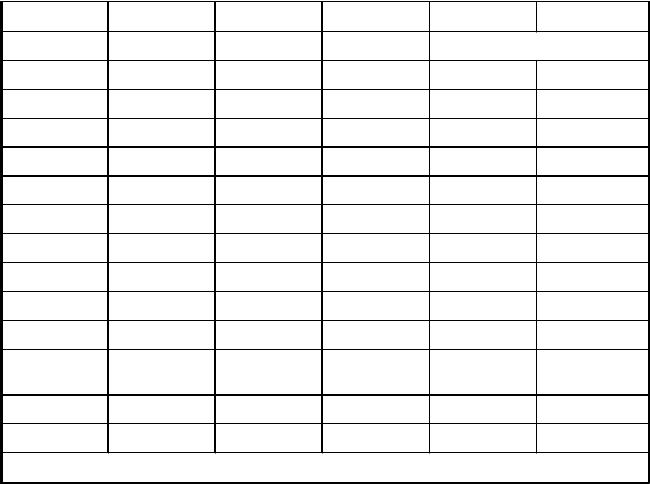
Пример решения обратной засечки по вышеприведенной методике приведен в табл. 1.
Решение обратной геодезической засечки с использование формулы Деламбра
Обратная угловая засечка в геодезических измерениях
Засечкой называют относительно простой метод вычисления координат некоторой точки посредством измерения на ней углов и расстояний по направлению на уже закрепленные на местности контуры.
К ней достаточно часто прибегают в различных геологических, строительных и инженерных работах за счет ее простоты и экономичности. На практике обратная засечка чаще всего используются для вычисления координат пунктов геодезической сети, выноса в натуру проектных точек и т.д.
Опытный геодезист сможет без труда провести нужные измерения при помощи теодолита, тахеометра или любого другого прибора всего за пару минут.
Виды засечек
В зависимости от местности и способов построения сетей сгущения в геодезии существует два основных вида привязки к опорным пунктам:
- Непосредственная. Подразумевает привязку теодолитного или полигонометрического хода к триангуляционным пунктам высшего класса с возможностью выполнить измерения примычных углов. Используется в тех случаях, когда на опорных точках можно выполнить те же измерения, что и на соседних.
- Косвенная. Проводится только при отсутствии возможности провести непосредственные измерения примычных длин и углов. К этому виду привязки и относится засечка.
По способу же построения геодезическая засечка бывает:
- линейной (полярные и биполярные по числу пунктов);
- угловой (прямая и обратная);
- комбинированной (положение точки определяют по известным углам и линейным расстояниям).
В геодезии чаще всего прибегают к комбинированию прямой и обратной засечек. Кроме того, чтобы полученные результаты были наиболее достоверными, измеряют больше величин, чем нужно, а само местоположение искомых пунктов получают посредством уравнивания.
Однократная и многократная засечка
Если для определения координат берется только один исходный пункт, то такая засечка будет называться однократной, а если более трех – многократной.
В основе обратной однократной угловой засечки лежит так называемая задача Потенота, которая была названа в честь французского математика Лорана Потенота, удачно решившего ее еще в 1692 году. Ученый предложил по известным значениям трех близлежащих точек вычислять координаты искомой.
На сегодняшний день существует уже более ста вариаций ее решения, которые были предложены многими именитыми учеными, но в геодезической практике наибольшую популярность получили формулы Жана Деламбра, Кнейссля и Гаусса.
Рисунок 1. Обратная многократная засечка
Важно отметить, что достоверные данные удается получить только в тех случаях, когда искомая точка находится в пределах треугольника, который образовали исходные пункты или же вне его, но напротив одной из его вершин.
Если же искомая точка попадает в пределы окружности, проходящей через эти точки, она становится неопределяемой. Этот ключевой недостаток в задаче Потенота, именуемый опасным кругом, приводит к необходимости определения дополнительной точки.
Обратная многократная угловая засечка как раз и подразумевает определение местоположения пункта через измерения на этом самом пункте углов или направлений как минимум на четыре твердых пункта, чьи координаты установлены. Этот метод более трудоемкий, но гарантирует надежный контроль результатов измерений. При обработке данных используют метод Гаусса-Ньютона, который в геодезии также называют параметрическим.
Способ Деламбра
Решение обратной засечки при помощи этого способа выполняется в такой последовательности:
- Вычисляется дирекционный угол исходного направления с отметки 1 на точку «0» по формуле обратной геодезической засечки:
Значения дирекционных углов с исходных отметок Т2, Т3, Т4 получают из формул:
Создавайте будущее вместе с нами
Присоединяйтесь к нашей команде: мы создаем финтех-сервисы для 28 млн клиентов и опережаем рынок на 5 лет. Работаем на результат и делаем больше, чем от нас ждут.
Способ Кнейссля
Аналогично способу Деламбра последовательность формул при решении задачи обратной геодезической засечки по Кнейсслю будет иметь следующий вид:
- Определяются вспомогательные коэффициенты:
Вычисляется котангенс дирекционного угла исходного направления на заданный пункт:
Приращения координаты точки Р относительно исходного пункта 1 находят при помощи нижеприведенных формул:
\(\Delta x_<1-p>=c\cdot \Delta y_<1-p>\)
Определяются координаты точки Р:
\(y_
=y_<1>+\Delta y_<1-p>\)
Средняя квадратическая погрешность вычисления местоположения пункта Р по трем направлениям вычисляется при помощи выражения:
Оценивается точность обратной угловой засечки по способу Кнейссля с определением погрешности:
Допустимость в расхождениях полученных значений двух вариантов решений выполняется по формуле:
Если данное условие соблюдено, то итоговое значение координат берется как среднее арифметическое значение из результатов двух решений.
Уравнивание при помощи параметрического способа
Под определение обратной многократной угловой засечки попадает как совокупность простых однократных измерений, так и просто большое количество избыточных. Однако в обоих случаях необходимо уравнивание, которое выполняется по измеренным углам и направлениям.
К примеру, неизвестные \(x_
\) и \(y_
\) – координаты точки Р, которые в данном способе будут представлены в качестве параметров. Для этого их представляют в виде приближенных значений \(x_<0>\), \(y_<0>\) и поправок к ним \(δх\) и \(δу\).
В приведенном уравнении \(x_<0>\) и \(y_<0>\) – результаты обработки однократных засечек, а \(δх\) и \(δу\) получают через уравнивание методом наименьших квадратов параметрическим способом с применением дифференциальных формул.
Этот метод подразумевает применение не только параметрического, но и коррелатного способа. Они дают одинаковые результаты, но отличаются по объему вычислений.
Однако в геодезической практике целесообразнее применять параметрический способ, поскольку при любом количестве избыточных измерений число нормальных уравнений будет аналогично числу неизвестных. При этом каждое неизвестное будет представлено в виде суммы приближенного значения и его поправки.
Сферы применения
Обратная угловая засечка нашла широкое применение в строительстве высотных зданий и сооружений, вроде опорных конструкций для мостов и дымовых труб. Кроем того, она позволяет быстро построить строительную сетку или определить местоположение точки в пространстве. В геодезии ее нередко используют в трилатерации и триангуляции.
Нельзя также не упомянуть ее огромного практического значения в навигации и военном деле. В частности, засечка по обратным дирекционным углам используется для топографогеодезической подготовки командно-наблюдательного пункта и позиции ведения огня.
Обратная геодезическая засечка
Обратная геодезическая засечка заключается в определении координат дополнительной точки М (рис. 12.2) путем измерения на этой точке углов между направлениями на три данных пункта и более с известными координатами. Полное решение этой задачи было разработано французским математиком Лорано Потенотом, поэтому определение координат точки методом обратной засечки часто называются задачей Потенота.
Рисунок 12.2 – Обратная угловая засечка
При использовании обратной засечки для привязки теодолитных или тахеометрических ходов к пунктам геодезической опорной сети необходимо измерить дополнительно примычной угол на определяемой точке. Кроме классического способа Потенота существует много различных способов решения обратной засечки.
12.2.1 Решение обратной засечки по трем исходным пунктам по полной схеме. Пусть даны координаты пунктов А, В и С; измерены горизонтальные углы a и b. Требуется определить координаты точки М. Ход решения:
Далее определяем координаты точки М дважды: относительно точки А и относительно точки С для контроля вычислений.
12.2.2 Решение по упрощенной форме.


12.2.3 Решение по промежуточной схеме (рис. 12.3).
Рисунок 12.3 – Обратная угловая засечка
Контроль: 
ТАХЕОМЕТРИЧЕСКАЯ СЪЕМКА

Картограммы и картодиаграммы Картограммы и картодиаграммы применяются для изображения географической характеристики изучаемых явлений.

Практические расчеты на срез и смятие При изучении темы обратите внимание на основные расчетные предпосылки и условности расчета.

Функция спроса населения на данный товар Функция спроса населения на данный товар: Qd=7-Р. Функция предложения: Qs= -5+2Р,где.

Аальтернативная стоимость. Кривая производственных возможностей В экономике Буридании есть 100 ед. труда с производительностью 4 м ткани или 2 кг мяса.
Индекс гингивита (PMA) (Schour, Massler, 1948) Для оценки тяжести гингивита (а в последующем и регистрации динамики процесса) используют папиллярно-маргинально-альвеолярный индекс (РМА).
Методика исследования периферических лимфатических узлов. Исследование периферических лимфатических узлов производится с помощью осмотра и пальпации.
Роль органов чувств в ориентировке слепых Процесс ориентации протекает на основе совместной, интегративной деятельности сохранных анализаторов, каждый из которых при определенных объективных условиях может выступать как ведущий.
Йодометрия. Характеристика метода Метод йодометрии основан на ОВ-реакциях, связанных с превращением I2 в ионы I- и обратно.
Броматометрия и бромометрия Броматометрический метод основан на окислении восстановителей броматом калия в кислой среде.
Метод Фольгарда (роданометрия или тиоцианатометрия) Метод Фольгарда основан на применении в качестве осадителя титрованного раствора, содержащего роданид-ионы SCN.